卷积
卷积和互相关
卷积的数学定义
在信号/图像处理领域,卷积的数学定义如下:
$$
(f{\star}g)(t)=\int_{-\infty}^{\infty}f(\theta)g(t-\theta)d\theta
$$
如上式,两函数卷积被定义为一函数反转后偏移对应位置之后计算两函数围成的封闭区域面积。
如上图,g函数为滤波器,g函数进行了翻转。
卷积的优点
- 权值共享
- 平移不变性
- 保留了空间相邻位置的相关性
互相关
互相关的数学定义如下:
$$
(f☆g)(t)=\int_{-\infty}^{\infty}f(\theta)g(\theta-t)d\theta
$$
可以看出互相关没有对滤波器函数的翻转。
互相关的物理意义是:一个向量在另一个向量上的投影。
卷积和互相关的联系与区别
卷积和互相关都是一种运算,唯一的区别就是卷积需要翻转“核函数”。
卷积具备交换律、分配律、结合律,而互相关只具备结合律。
其实在深度学习中,卷积神经网络并没有使用卷积,而是互相关操作,其原因是卷积核是不断学习更新的。
如果在卷积的过程中学习,则可以最终学习到目标卷积核,反之如果互相关,则学到的是目标卷积核的翻转结果。
而学习到的结果是目标卷积核还是其翻转结果,理论上包含的信息是一致的,但是互相关的对应关系更加直观,所以我们直接用互相关操作即可达到效果。
但是在应用当中,互相关运算主要描述信号与信号之间的关系,而卷积运算主要描述的是信号与系统之间的关系,所以命名上,我们还是叫卷积神经网络。
卷积
1-D卷积
1-D full卷积
输入向量每一个点同kernel的每一个点相乘过,相当于步长为1,0填充$k-1$(k为kernel的长度)的卷积。
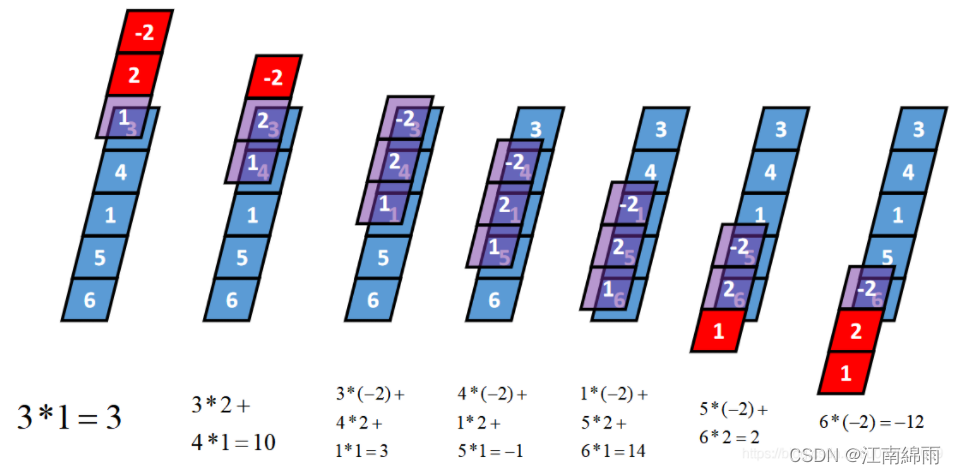
1-D Same卷积
不改变向量的长度,相当于步长为1,0填充$\frac{k-1}{2}$(k为kernel的长度)的卷积。
1-D Valid卷积
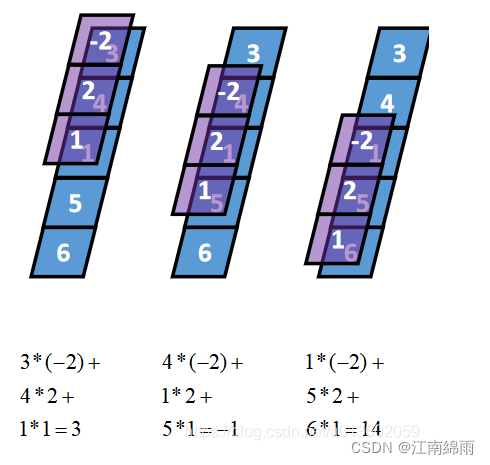
我们一般认为的卷积,相当于步长为1,0填充0的卷积。
2-D卷积
单通道
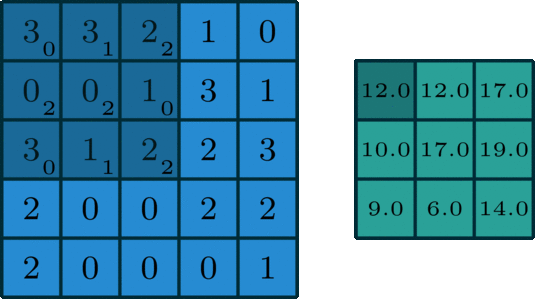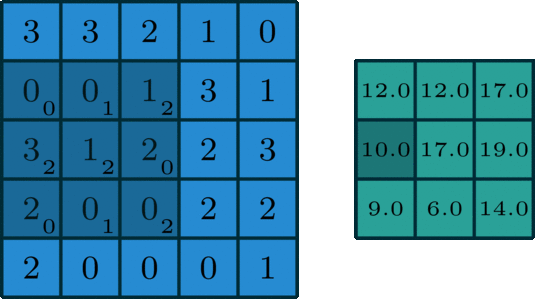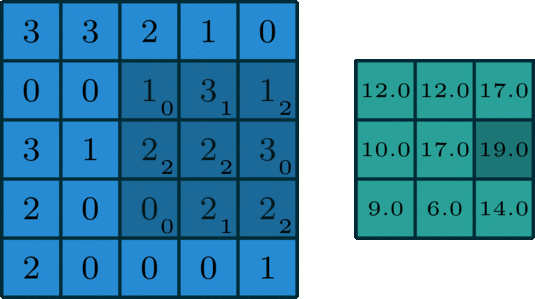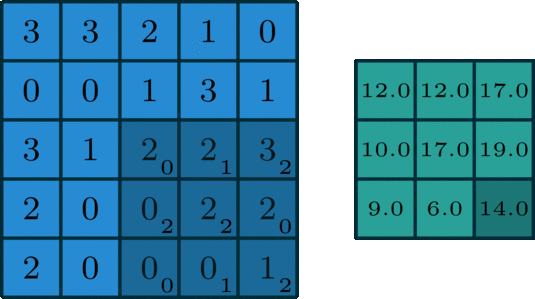
如上所示,是一种类似滑动窗口的方式,不再赘述。
记住步长和填充的含义,会计算卷积后的尺寸(维度),如下式:
$$
o = lower_bound(\frac{i+2p-k}{s})+1
$$
多通道
类似,也是对应的位置作积,最后将相同的位置全部相加得到二维数组,如下:
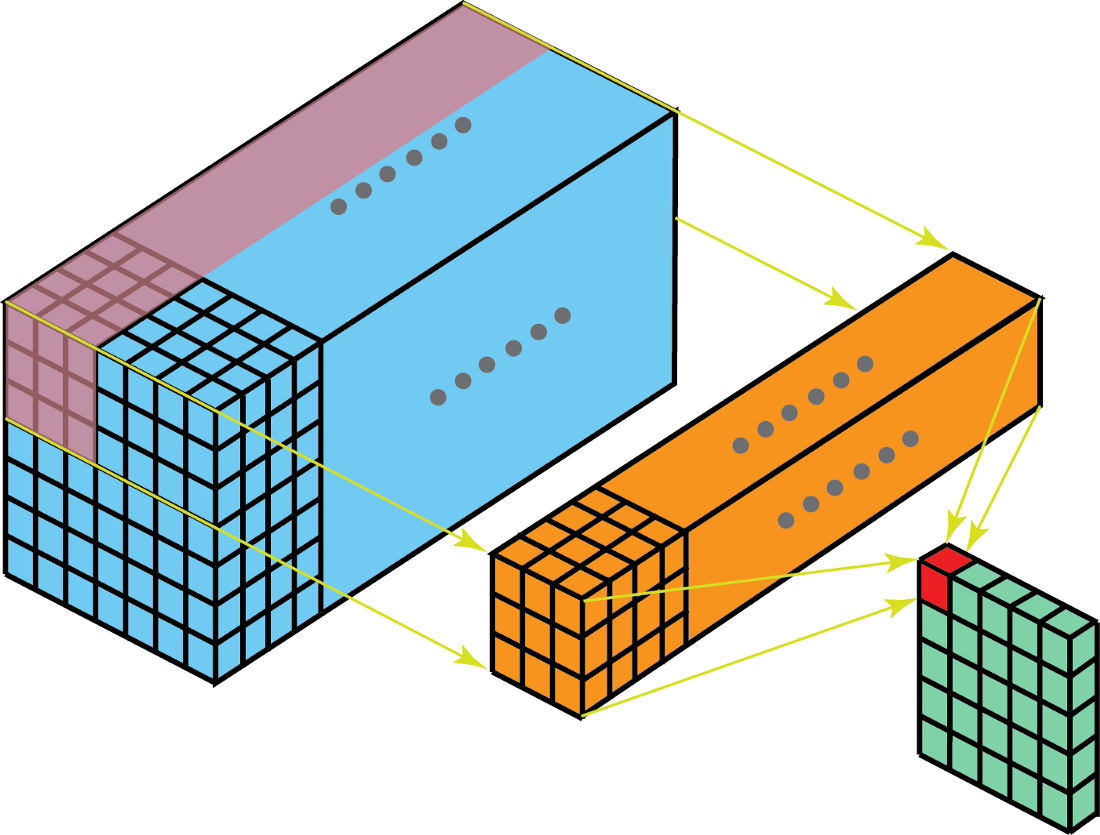
核与滤波器
核是指一个二维权重数组,滤波器一般指堆叠在一起的多个核的三维结构。通道与核并列,而层与滤波器并列。
,如此可保证输出一个2-D的数组。
3-D卷积
如下图,不再赘述:
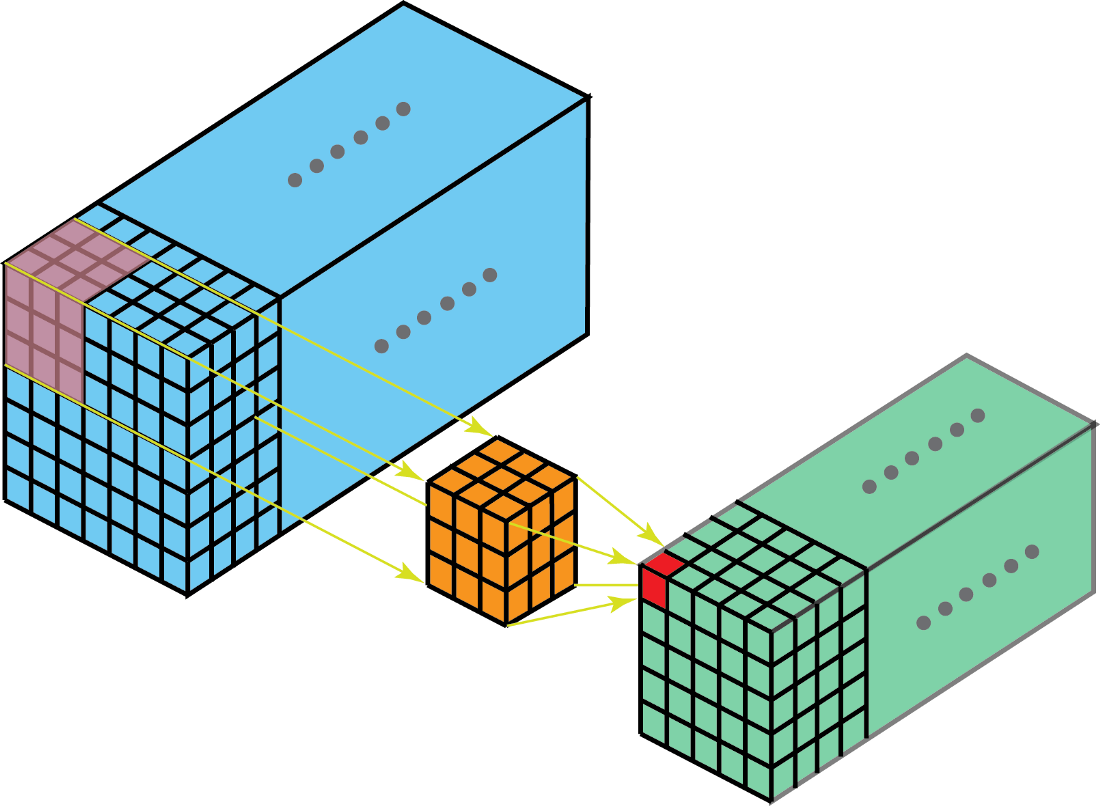
特殊卷积
1x1卷积
滤波器核的大小为1*1*D。
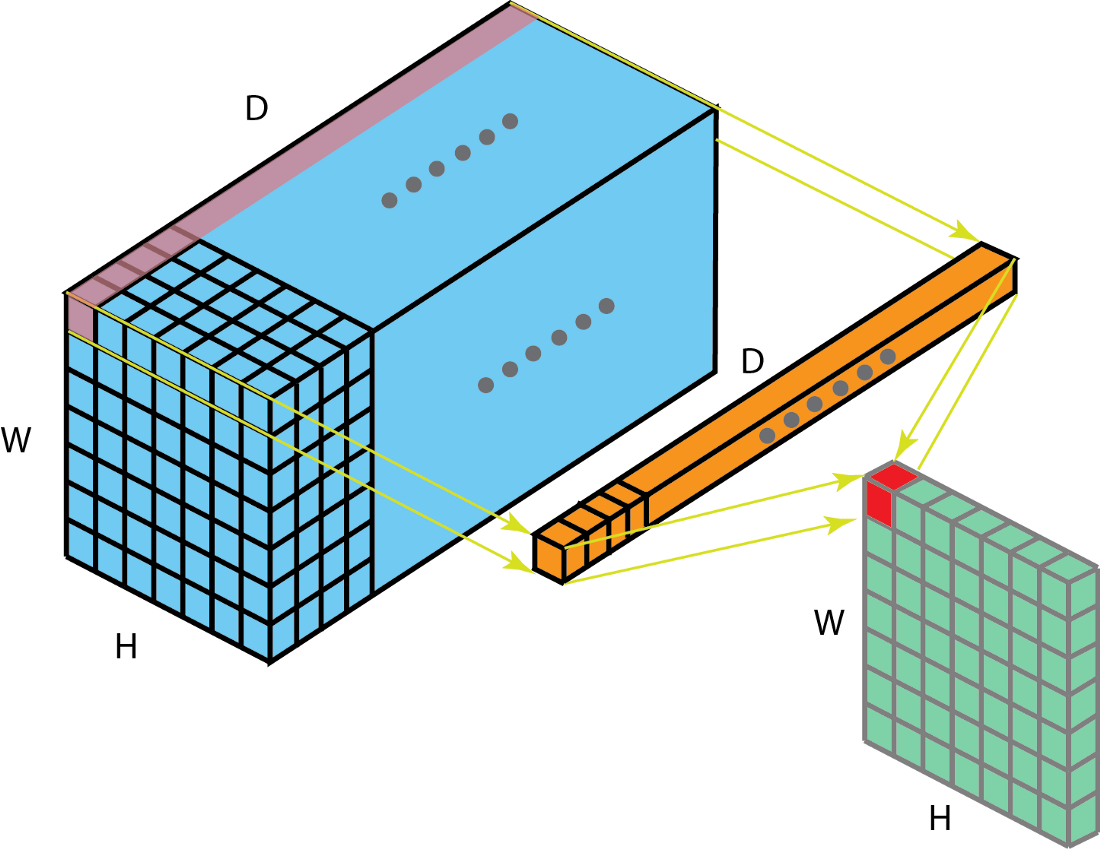
- 有效减少维度
- 有效低维嵌入
- 卷积后再应用非线性
转置卷积(反卷积)
转置卷积的目的是上采样信号。转置卷积又称反卷积,但这里的反卷积并不是信号/图像处理中的逆转了卷积操作的“反卷积”操作。所以反卷积这个称呼并不正确。更加符合认知的称呼是“小数步长卷积”
如下是转置卷积的操作:
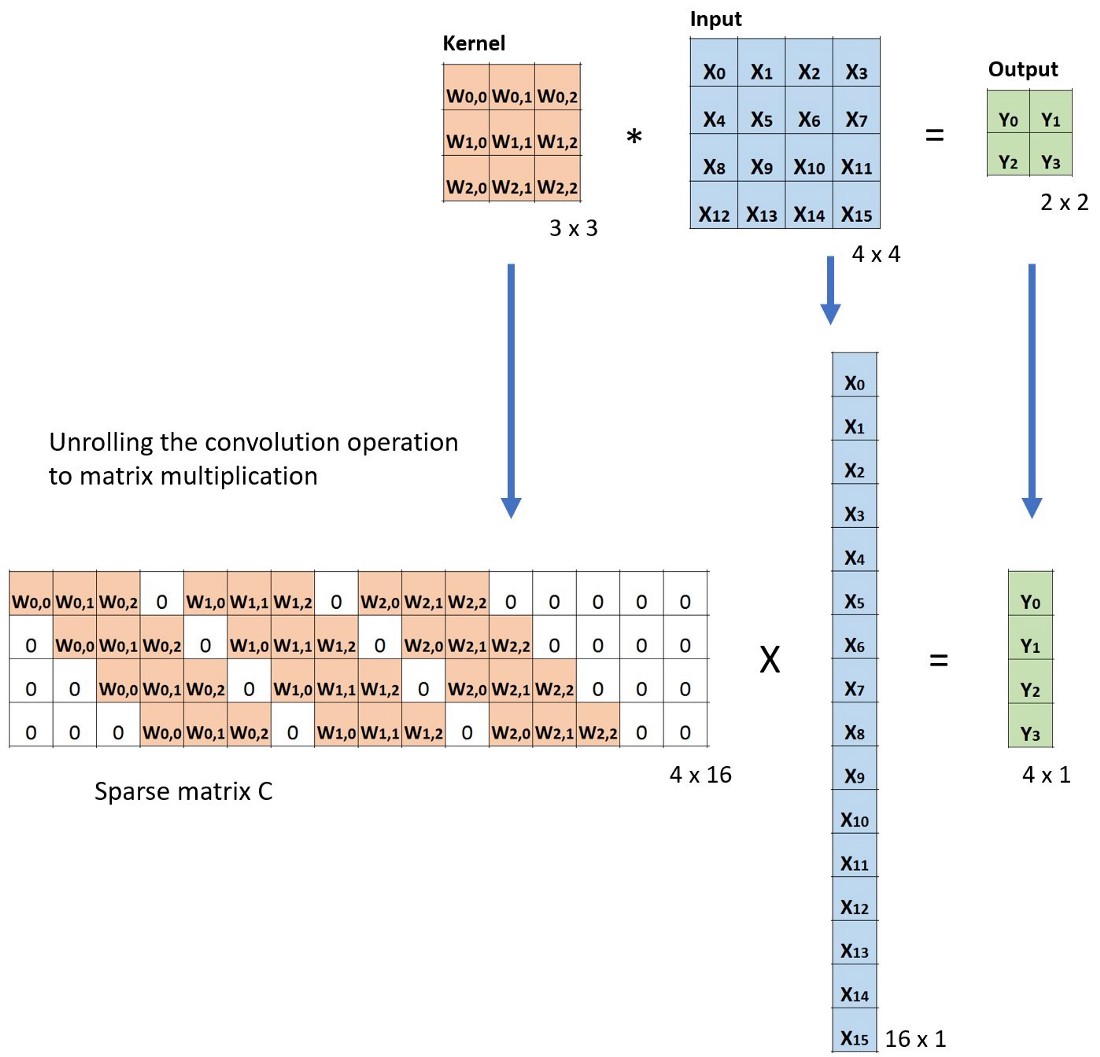
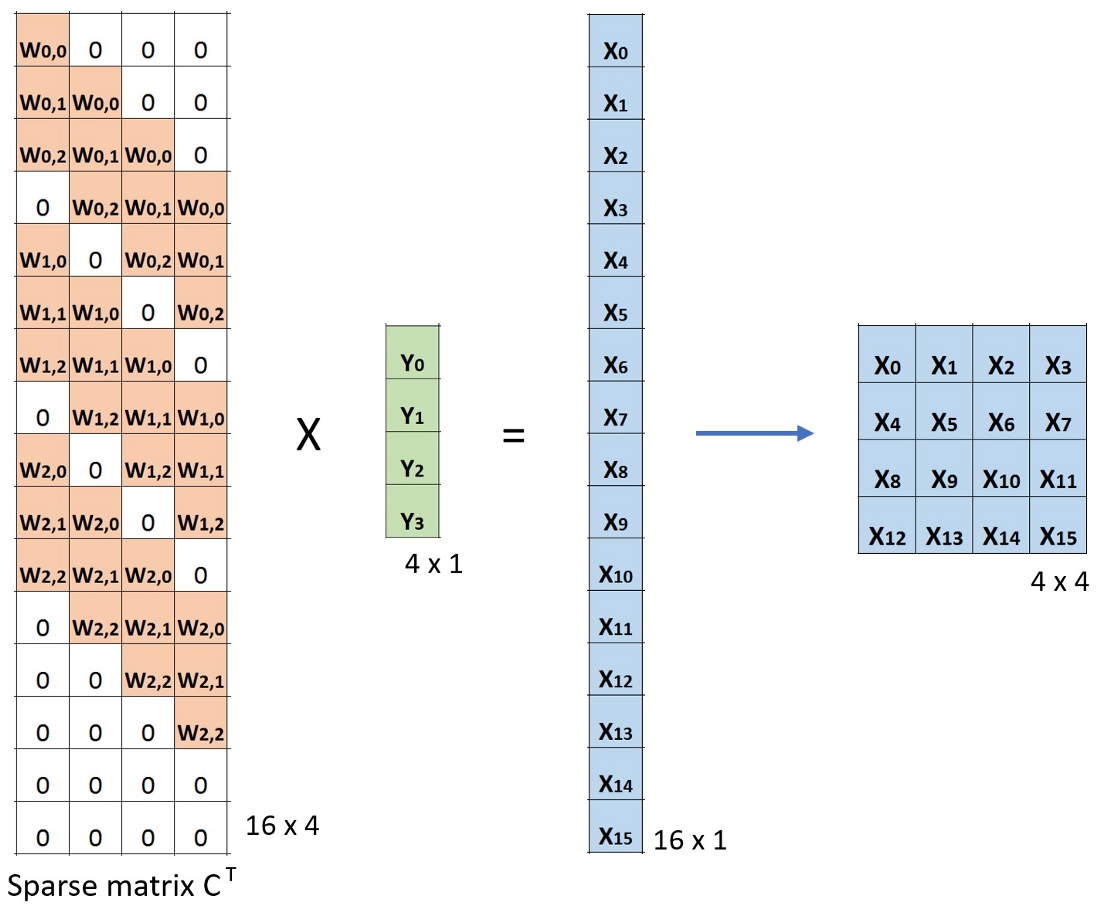
转置卷积的问题
会出现棋盘伪影:转置卷积造成的部分像素得到了信息的“重叠”,如下所示:
空洞卷积
空洞卷积在kernel元素之间插入空格,这时需要一个额外的参数膨胀率l,向元素之间插入l-1个空格。
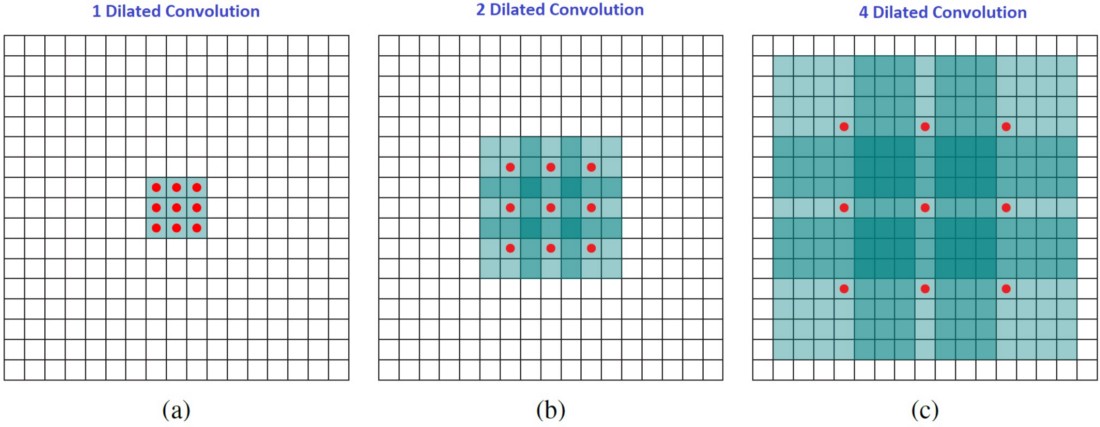
优点:计算量小、参数少、感受野大
缺点:损失信息连续性、远距离信息可能不相关
改进:混合空洞卷积
可分离卷积
MobileNet、Xception中有使用。
空间可分离卷积
空间可分离卷积是利用了某些卷积核可以拆分成两个行、列向量相乘。这样就可以把一个2-D卷积操作变成两组1-D卷积操作。
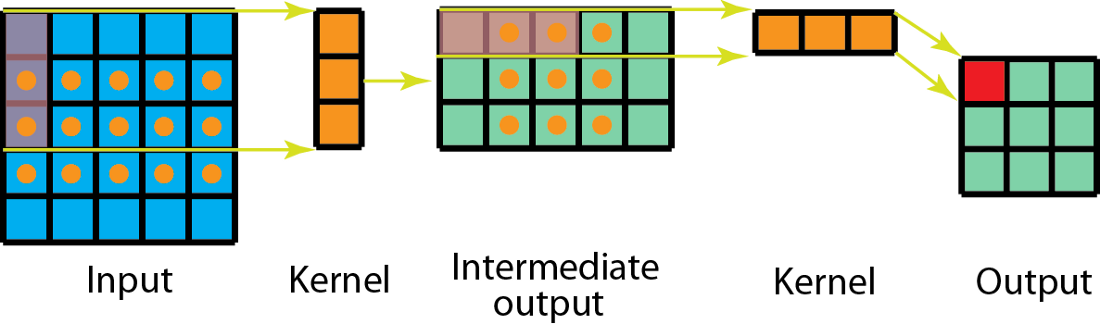
这样可以减少计算量,证明略。但是我们在深度学习中却很少使用,原因是所求的最优kernel并不一定是可拆分的。
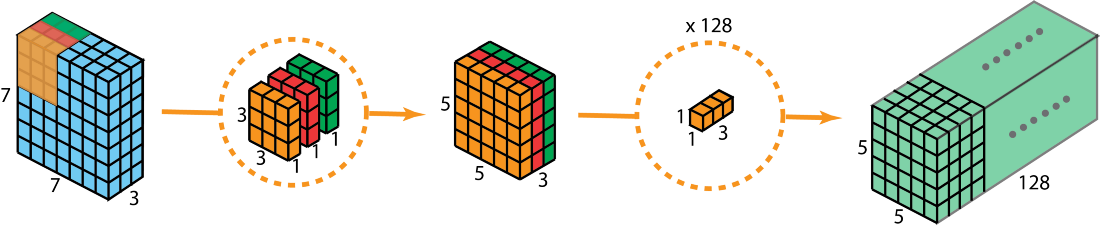
深度可分离卷积
depthwise卷积+1x1卷积,等效于一次3-D卷积。
扁平卷积

类似于可分离卷积,将3-D卷积的滤波器拆分为三个1-D核各自卷积。所以优缺点也同上空间可分离卷积。
分组卷积
分组卷积是将输入张量根据深度分成n组,每组与Dout/n个深度Din/n的滤波器进行简单的2-D卷积之后连接得到。
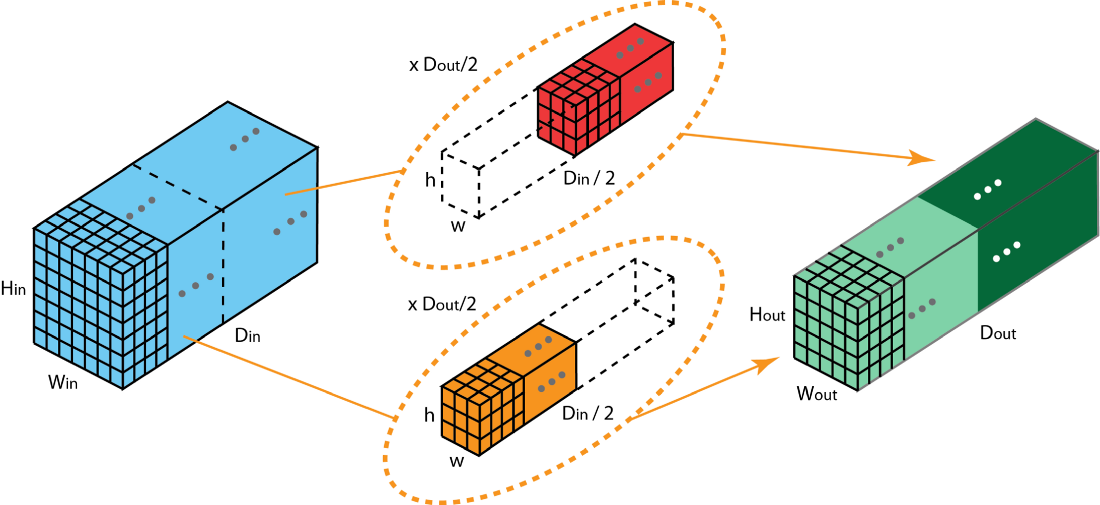
优点:并行化效果更加好、参数量少、模型效果好。
混洗分组卷积
包括分组卷积和通道混洗,所谓通道混洗大概意思就是在做分组卷积前,将各个分组的通道进行混合,这样有利于分组间的特征可以流动,这样特征表示得到增强。
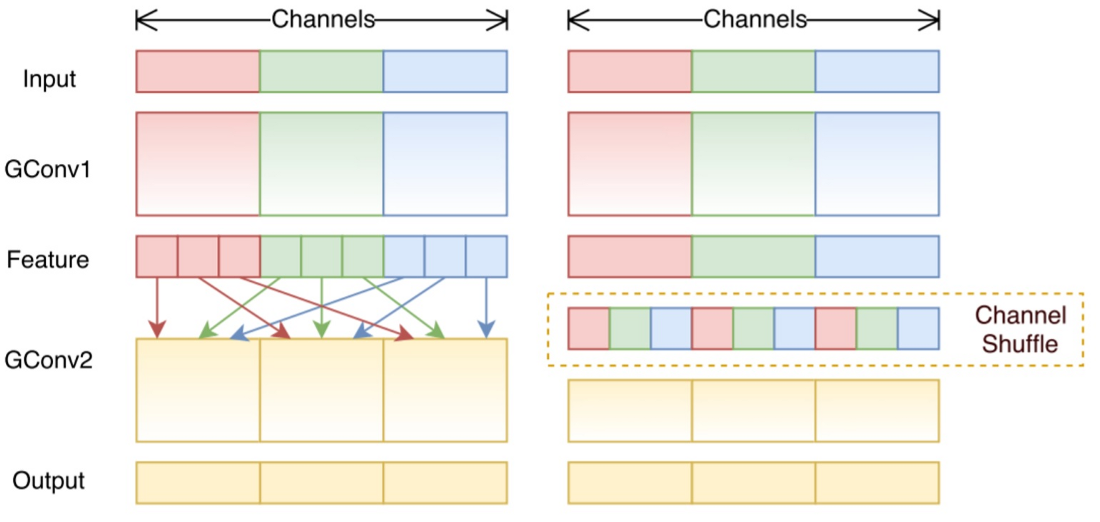
逐点分组卷积
用于ShuffleNet。将深度可分离卷积第一步depthwise卷积的分组卷积替换为1x1卷积,之后进行1X1卷积即可。
Reference
CS131专题-1:卷积、互相关_⊙月的博客-CSDN博客_卷积互相关
